$$$$

2  $★$ Dubious Computations

We already saw, when visiting infinite processes from antiquity, that it is very easy to get confused and derive a contradiction when working with infinity. But on the other hand, infinite arguments turn out to be so useful that they are irresistible! Certain objects, like $\pi$, seem to be all but out of reach without invoking infinity somewhere, and while the lessons of the ancients implore us to be careful, more than once a good mathematician has thrown caution to the wind, in the hopes of gazing upon startling new truths.

2.1 Convergence, Concern and Contradiction

2.1.1 Madhava, Leibniz & $\pi /4$

Madhava was a Indian mathematician who discovered many infinite expressions for trigonometric functions in the 1300’s, results which today are known as Taylor Series after Brook Taylor, who worked with them in 1715. In a particularly important example, Madhava found a formula to calculate the arc length along a circle, in terms of the tangent: or phrased more geometrically, the arc of a circle contained in a triangle with base of length $1$.

The first term is the product of the given sine and radius of the desired arc divided by the cosine of the arc. The succeeding terms are obtained by a process of iteration when the first term is repeatedly multiplied by the square of the sine and divided by the square of the cosine. All the terms are then divided by the odd numbers 1, 3, 5, …. The arc is obtained by adding and subtracting respectively the terms of odd rank and those of even rank.

As an equation, this gives

$$\theta =\frac{\sin \theta }{\cos \theta }-\frac{1}{3}\frac{{\sin }^2\theta }{{\cos }^2\theta }\left(\frac{\sin \theta }{\cos \theta }\right)+\frac{1}{5}\frac{{\sin }^2\theta }{{\cos }^2\theta }\left(\frac{{\sin }^2\theta }{{\cos }^2\theta }\frac{\sin \theta }{\cos \theta }\right)+\cdots$$

$$=\tan \theta -\frac{{\tan }^3\theta }{3}+\frac{{\tan }^5\theta }{5}-\frac{{\tan }^7\theta }{7}+\frac{{\tan }^9\theta }{9}-\cdots$$

If we take the arclength $\pi /4$ (the diagonal of a square), then both the base and height of our triangle are equal to $1$, and this series becomes

$$\frac{\pi }{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots$$

This result was also derived by Leibniz (one of the founders of modern calcuous), using a method close to something you might see in Calculus II these days. It goes as follows: we know (say from the last chapter) the sum of the geometric series

$$\sum _{n\ge 0}{r}^n=\frac{1}{1-r}$$

Thus, substituting in $r=-x^2$ gives

$$\sum _{n\ge 0}(-1{)}^n{x}^{2n}=\frac{1}{1+x^2}$$

and the right hand side of this is the derivative of arctangent! So, anti-differentiating both sides of the equation yields

$$\begin{array}{rl}\arctan x& =\int \sum _{n\ge 0}(-1{)}^n{x}^{2n}dx\\ & =\sum _{n\ge 0}\int (-1{)}^n{x}^{2n}dx\\ & =\sum _{n\ge 0}(-1{)}^n\frac{x^{2n+1}}{2n+1}\end{array}$$

Finaly, we take this result and plug in $x=1$: since $\arctan (1)=\pi /4$ this gives what we wanted:

$$\frac{\pi }{4}=\sum _{n\ge 0}(-1{)}^n\frac{1}{2n+1}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots$$

This argument is completely full of steps that should make us worried:

• Why can we substitute a variable into an infinite expression and ensure it remains valid?
• Why is the derivative of arctan a rational function?
• Why can we integrate an infinite expression?
• Why can we switch the order of taking an infinte sum, and integration?
• How do we know which values of $x$ the resulting equation is valid for?

But beyond all of this, we should be even more worried if we try to plot the graphs of the partial sums of this supposed formula for the arctangent.

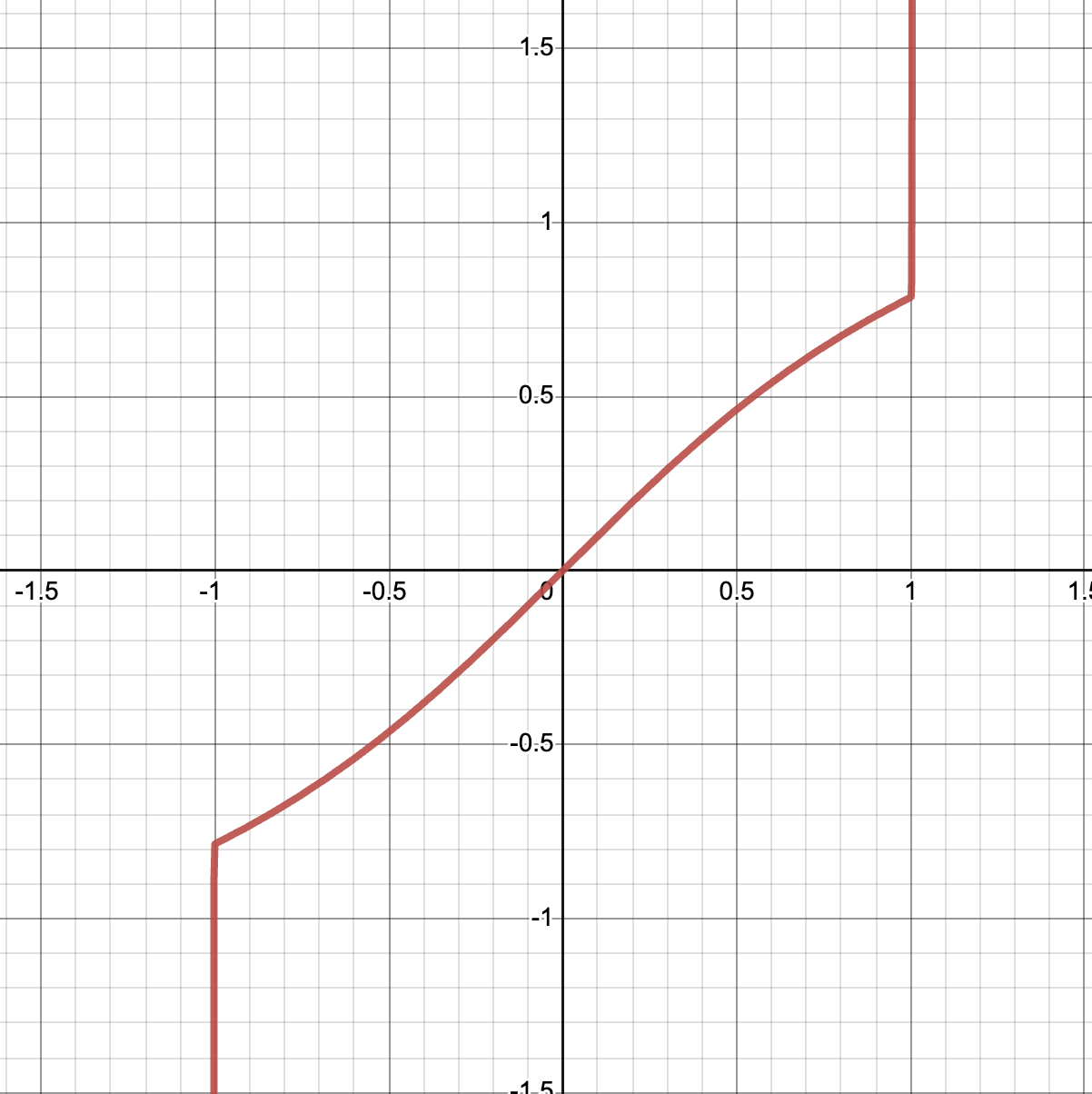
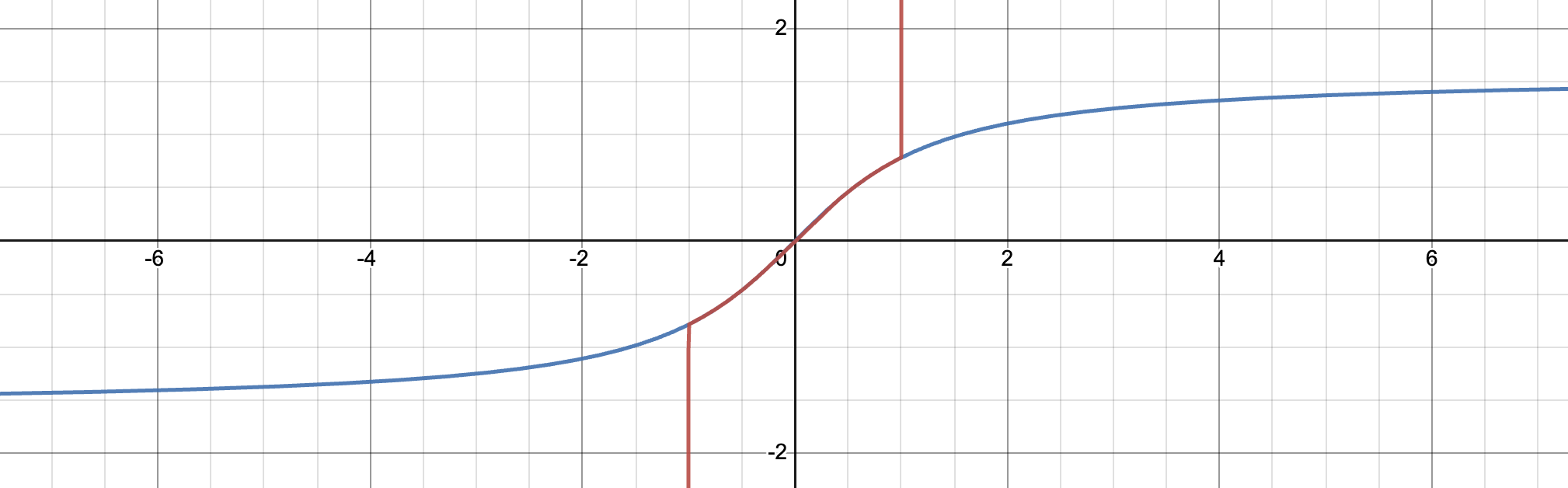
The infinite series we derived seems to match the arctangent exactly for a while, and then abruptly stop, and shoot off to infinity. Where does it stop? *Right at the point we are interested in, $\theta =\pi /4$, so $\tan (\theta )=1$. So, even a study of which intervals a series converges in will not be enough here, we need a theory that is so precise, it can even tell us exactly what happens at the single point forming the boundary between order and chaos.

And perhaps, before thinking the eventual answer might simply say the series always converges at the endpoints, it turns out at the other endpoint $x=-1$, this series itself diverges! So whatever theory we build will have to account for such messy cases.

2.1.2 Dirichlet & $\log 2$

In 1827, Dirichlet was studying the sums of infinitely many terms, thinking about the alternating harmonic series $$\sum _{n\ge 1}\frac{(-1{)}^n}{n+1}$$

Like the previous example, this series naturally emerges from manipulations in calculus: beginning once more with the geometric series $\sum _{n\ge 0}{r}^n=\frac{1}{1-r}$. We substitute $r=-x$ to get a series for $1/(1+x)$ and then integrate term by term to produce a series for the logarithm:

$$\log (1+x)=\int \frac{1}{1+x}dx=\int \sum _{n\ge 0}(-1{)}^n{x}^n$$

$$=\sum _{n\ge 0}(-1{)}^n\frac{x^{n+1}}{n+1}=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\cdots$$

Finally, plugging in $x=1$ yields the sum of interest. It turns out not to be difficult to prove that this series does indeed approach a finite value after the addition of infinitely many terms, and a quick check adding up the first thousand terms gives an approximate value of $0.6926474305598$, which is very close to $\log (2)$ as expected..

$$\log (2)=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\frac{1}{7}-\frac{1}{8}+\frac{1}{9}-\frac{1}{10}\cdots$$

What happens if we multiply both sides of this equation by $2$?

$$2\log (2)=2-1+\frac{2}{3}-\frac{1}{2}+\frac{2}{5}-\frac{1}{3}+\frac{2}{7}-\frac{1}{4}+\frac{2}{9}-\frac{1}{5}\cdots$$

We can simplify this expression a bit, by re-ordering the terms to combine similar ones:

$$\begin{array}{rl}2\log (2)& =(2-1)-\frac{1}{2}+(\frac{2}{3}-\frac{1}{3})-\frac{1}{4}+(\frac{2}{5}-\frac{1}{5})-\cdots \\ & =1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\cdots \end{array}$$

After simplifying, we’ve returned to exactly the same series we started with! That is, we’ve shown $2\log (2)=\log (2)$, and dividing by $\log (2)$ (which is nonzero!) we see that $2=1$, a contradiction!

What does this tell us? Well, the only difference between the two equations is the order in which we add the terms. And, we get different results! This reveals perhaps the most shocking discovery of all, in our time spent doing dubious computations: infinite addition is not always commutative, even though finite addition always is.

Here’s an even more dubious-looking example where we can prove that $0=\log 2$. First, consider the infinite sum of zeroes:

$$0=0+0+0+0+0+\cdots$$

Now, rewrite each of the zeroes as $x-x$ for some specially chosen $x$s:

$$0=(1-1)+(\frac{1}{2}-\frac{1}{2})+(\frac{1}{3}-\frac{1}{3})+(\frac{1}{}-\frac{1}{4})+\cdots$$

Now, do some re-arranging to this:

$$(1+\frac{1}{2}-1)+(\frac{1}{3}+\frac{1}{4}-\frac{1}{2})+(\frac{1}{5}+\frac{1}{6}-\frac{1}{3})+\cdots$$

Make sure to convince yourselves that all the same terms appear here after the rearrangement!

Simplifying this a bit shows a pattern:

$$(1-\frac{1}{2})+(\frac{1}{3}-\frac{1}{4})+(\frac{1}{5}-\frac{1}{6})+\cdots$$

Which, after removing the parentheses, is the familiar series $\sum \frac{(-1{)}^n}{n}$. But this series equals $\log (2)$ (or, was it $2\log 2$?) So, if we are to believe that arithmetic with infinite sums is valid, we reach the contradiction

$$0=\log 2$$

2.2 Infinite Expressions for $\sin (x)$

The sine function (along with the other trigonometric, exponential, and logarithmic functions) differs from the common functions of early mathematics (polynomials, rational functions and roots) in that it is defined not by a formula but geometrically.

Such a definition is difficult to work with if one actually wishes to compute: for example, Archimedes after much trouble managed to calculate the exact value of $\sin (\pi /96)$ using a recursive doubling procedure, but he would have failed to calculate $\sin (\pi /97)$ - 97 is not a multiple of a power of 2, so his procedure wouldn’t apply! The search for a general formula that you could plug numbers into and compute their sine, was foundational to the arithmetization of geometry.

2.2.1 Infinite Sum of Madhava

Beyond the series for the arctangent, Madhava also found an infinite series for the sine function. The first thing that needs to be proven is that $\sin (x)$ satisfies the following integral equation: (Check this, using your calculus knowledge!) $$\sin (\theta )=\theta -{\int }_0^{\theta }{\int }_0^t\sin (u)dudt$$

This equation mentions sine on both sides, which means we can use it as a recurrence relation to find better and better approximations of the sine function.

Definition 2.1 (Integral Recurrence For $\sin (x)$.) We define a sequence of functions $s_n(x)$ recursively as follows:

$$s_{n+1}(\theta )=\theta -{\int }_0^{\theta }{\int }_0^t{s}_n(u)dudt$$

Given any starting function $s_0(x)$, applying the above produces a sequence $s_1(x)$, $s_2(x)$, $s_3(x),\dots$ which we will use to approximate the sine function.

Example 2.1 (The Series for $\sin (x)$) Like any recursive procedure, we need to start somewhere: so let’s begin with the simplest possible (and quite incorrect) “approximation” that $s_0(\theta )=0$. Integrating this twice still gives zero, so our first approximation is $$s_1(\theta )=\theta -{\int }_0^{\theta }{\int }_0^{t}0dudt=\theta -0=\theta$$

Now, plugging in $s_1=\theta$ yields our second approximation: $$\begin{array}{rl}{s}_2(\theta )& =\theta -{\int }_0^{\theta }{\int }_0^{t}ududt\\ & =\theta -{\int }_0^{\theta }\frac{u^2}{2}{|}_0^{t}dt\\ & =\theta -{\int }_0^{\theta }\frac{t^2}{2}dt\\ & =\theta -\frac{t^3}{3\cdot 2}{|}_0^{\theta }\\ & =\theta -\frac{{\theta }^3}{3!}\end{array}$$

Repeating gives the third,

$$\begin{array}{rl}{s}_3(\theta )& =\theta -{\int }_0^{\theta }{\int }_0^t(u-\frac{u^3}{3})dudt\\ & =\theta -{\int }_0^{\theta }(\frac{t^2}{2}-\frac{t^4}{4\cdot 3!})dt\\ & =\theta -(\frac{{\theta }^3}{3\cdot 2}-\frac{{\theta }^5}{5\cdot 4\cdot 3!})\\ & =\theta -\frac{{\theta }^3}{3!}+\frac{{\theta }^5}{5!}\end{array}$$

Carrying out this process infinitely many times yields a conjectured formula for the sine function as an infinite polynomial:

Proposition 2.1 (Madhava Infinite Sine Series) $$\sin (\theta )=\theta -\frac{{\theta }^3}{3!}+\frac{{\theta }^5}{5!}-\frac{{\theta }^7}{7!}+\frac{{\theta }^9}{9!}-\frac{{\theta }^{11}}{11!}+\cdots$$

Exercise 2.1 Find a similar recursive equation for the cosine function, and use it to derive the first four terms of its series expansion.

One big question about this procedure is why in the world should this work? We found a function that $\sin (x)$ satisfies, and then we plugged something else into that function and started iterating: what justification do we have that this should start to approach the sine? We can check after the fact that it (seems to have) worked, but this leaves us far from any understanding of what is actually going on.

2.2.2 Infinite Product of Euler

Another infinite expression for the sine function arose from thinking about the behavior of polynomials, and the relation of their formulas to their roots. As an example consider a quartic polynomial $p(x)$ with roots at $x=a,b,c,d$. Then we can recover $p$ up to a constant multiple as a product of linear factors with roots at $a,b,c,d$. If the $y-$intercept is $p(0)=k$, we can give a fully explicit description

$$p(x)=k(1-\frac{x}{a})(1-\frac{x}{b})(1-\frac{x}{c})(1-\frac{x}{d})$$

In 17334, Euler attempted to apply this same reasoning in the infinite case to the trigonometric function $\sin (x)$. This has roots at every integer multiple of $\pi$, and so following the finite logic, should factor as a product of linear factors, one for each root. There’s a slight technical problem in directly applying the above argument, namely that $\sin (x)$ has a root at $x=0$, so $k=0$. One work-around is to consider the function $\frac{\sin x}{x}$. This is not actually defined at $x=0$, but one can prove $\underset{x\to 0}{lim}\frac{\sin x}{x}=1$, and attempt to use $k=1$

GRAPH

Its roots agree with that of $\sin (x)$ except there is no longer one at $x=0$. That is, the roots are $\dots ,-3\pi ,-2\pi ,-\pi ,\pi ,2\pi ,3\pi ,\dots$, and the resulting factorization is

$$\frac{\sin x}{x}=\cdots (1+\frac{x}{3\pi })(1+\frac{x}{2\pi })(1+\frac{x}{\pi })(1-\frac{x}{\pi })(1-\frac{x}{2\pi })(1-\frac{x}{3\pi })\cdots$$

Euler noticed all the factors come in pairs, each of which represented a difference of squares.

$$(1-\frac{x}{n\pi })(1+\frac{x}{2n\pi })=(1-\frac{x^2}{n^2{\pi }^2})$$

Not worrying about the fact that infinite multiplication may not be commutative (a worry we came to appreciate with Dirichlet, but this was after Euler’s time!), we may re-group this product pairing off terms like this, to yield

$$\frac{\sin x}{x}=(1-\frac{x^2}{{\pi }^2})(1-\frac{x^2}{2^2{\pi }^2})(1-\frac{x^2}{3^2{\pi }^2})\cdots$$

Finally, we may multiply back through by $x$ and get an infinite product expression for the sine function:

Proposition 2.2 (Euler) $$\sin x=x(1-\frac{x^2}{{\pi }^2})(1-\frac{x^2}{4{\pi }^2})(1-\frac{x^2}{9{\pi }^2})\cdots$$

This incredible identity is actually correct: there’s only one problem - the argument itself is wrong!

Exercise 2.2 In his argument, Euler crucially uses that if we know

• all the zeroes of a function
• the value of that function is 1 at $x=0$

then we can factor the function as an infinite polynomial in terms of its zeroes. This implies that a function is completely determined by its value at $x=0$ and its zeroes (because after all, once you know that information you can just write down a formula like Euler did!) This is absolutely true for all finite polynomials, but it fails spectacularly in general.

Show that this is a serious flaw in Euler’s reasoning by finding a different function that has all the same zeroes as $\sin (x)/x$ and is equal to $1$ at zero (in the limit)!

Exercise 2.3 (The Wallis Product for $\pi$) In 1656 John Wallis derived a remarkably beautiful formula for $\pi$ (though his argumnet was not very rigorous).

$$\frac{\pi }{2}=\frac{2}{1}\frac{2}{3}\frac{4}{3}\frac{4}{5}\frac{6}{5}\frac{6}{7}\frac{8}{7}\frac{8}{9}\frac{10}{9}\frac{10}{11}\frac{12}{11}\frac{12}{13}\cdots$$

Using Euler’s infinite product for $\sin (x)$ evaluated at $x=\pi /2$, give a derivation of Wallis’ formula.

2.2.3 The Basel Problem

The Italian mathematician Pietro Mengoli proposed the following problem in 1650:

Definition 2.2 (The Basel Problem) Find the exact value of the infinite sum $$1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}+\cdots$$

By directly computing the first several terms of this sum one can get an estimate of the value, for instance adding up the first 1,000 terms we find $1+\frac{1}{2^2}+\frac{1}{3^2}+\cdots \frac{1}{1,{000}^2}=1.6439345\dots$, and ading the first million terms gives

$$1+\frac{1}{2^2}+\frac{1}{3^2}+\cdots +\frac{1}{1,{000}^2}+\cdots +\frac{1}{1,000,{000}^2}=1.64492406\dots$$

so we might feel rather confident that the final answer is somewhat close to 1.64. But the interesting math problem isn’t to approximate the answer, but rather to figure out something exact, and knowing the first few decimals here isn’t of much help.

This problem was attempted by famous mathematicians across Europe over the next 80 years, but all failed. All until a relatively unknown 28 year old Swiss mathematician named Leonhard Euler published a solution in 1734, and immediately shot to fame. (In fact, this problem is named the Basel problem after Euler’s hometown.)

Proposition 2.3 (Euler) $$\sum _{n\ge 1}\frac{1}{n^2}=\frac{{\pi }^2}{6}$$

Euler’s solution begins with two different expressions for the function $\sin (x)/x$, which he gets from the sine’s series expansion, and his own work on the infinite product:

$$\begin{array}{rl}\frac{\sin x}{x}& =1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+\frac{x^8}{9!}-\frac{x^{10}}{11!}+\cdots \\ & =(1-\frac{x^2}{{\pi }^2})(1-\frac{x^2}{2^2{\pi }^2})(1-\frac{x^2}{3^2{\pi }^2})\cdots \end{array}$$

Because two polynomials are the same if and only if the coefficients of all their terms are equal, Euler attempts to generalize this to infinite expressions, and equate the coefficients for $\sin$. The constant coefficient is easy - we can read it off as $1$ from both the series and the product, but the quadratic term already holds a deep and surprising truth.

From the series, we can again simply read off the coefficient as $-1/3!$. But from the product, we need to think - after multiplying everything out, what sort of products will lead to a term with $x^2$? Since each factor is already quadratic this is more straightforward than it sounds at first - the only way to get a quadratic term is to take one of the quadratic terms already present in a factor, and multiply it by 1 from another factor! Thus, the quadratic terms are $-\frac{x^2}{2^2{\pi }^2}-\frac{x^2}{3^2{\pi }^2}-\frac{x^2}{4^2{\pi }^2}-\cdots$. Setting the two coefficients equal (and dividing out the negative from each side) yields

$$\frac{1}{3!}=\frac{1}{{\pi }^2}+\frac{1}{2^2{\pi }^2}+\frac{1}{3^2{\pi }^2}+\cdots$$

Which quickly leads to a solution to the original problem, after multiplying by ${\pi }^2$:

$$\frac{{\pi }^2}{3!}=1+\frac{1}{2^2}+\frac{1}{3^2}+\cdots$$

Euler had done it! There are of course many dubious steps taken along the way in this argument, but calculating the numerical value,

$$\frac{{\pi }^2}{3!}=1.64493406685\dots$$

We find it to be exactly the number the series is heading towards. This gave Euler the confidence to publish, and the rest is history.

But we analysis students should be looking for potential troubles in this argument. What are some that you see?

2.2.4 Viète’s Infinite Trigonometric Identity

Viete was a French mathematician in the mid 1500s, who wrote down for the first time in Europe, an exact expression for $\pi$ in 1596.

Proposition 2.4 (Viète’s formula for $\pi$) $$\frac{2}{\pi }=\frac{\sqrt{2}}{2}\frac{\sqrt{2+\sqrt{2}}}{2}\frac{\sqrt{2+\sqrt{2+\sqrt{2}}}}{2}\frac{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}{2}\cdots$$

Viete’s original publicaiton of this formula - it predates our modern notation for square roots!

How could one derive such an incredible looking expression? One approach uses trigonometric identities…an infinite number of times! Start with the familiar function $\sin (x)$. Then we may apply the double angle identity to rewrite this as

$$\sin (x)=2\sin \left(\frac{x}{2}\right)\cos \left(\frac{x}{2}\right)$$

Now we may apply the double angle identity once again to the term $\sin (x/2)$ to get

$$\begin{array}{rl}\sin (x)& =2\sin \left(\frac{x}{2}\right)\cos \left(\frac{x}{2}\right)\\ & =4\sin \left(\frac{x}{4}\right)\cos \left(\frac{x}{4}\right)\cos \left(\frac{x}{2}\right)\end{array}$$

and again

$$\sin (x)=8\sin \left(\frac{x}{8}\right)\cos \left(\frac{x}{8}\right)\cos \left(\frac{x}{4}\right)\cos \left(\frac{x}{2}\right)$$

and again

$$\sin (x)=16\sin \left(\frac{x}{16}\right)\cos \left(\frac{x}{16}\right)\cos \left(\frac{x}{8}\right)\cos \left(\frac{x}{4}\right)\cos \left(\frac{x}{2}\right)$$

And so on….after the $n^{th}$ stage of this process one can re-arrange the the above into the following (completely legitimate) identity:

$$\frac{\sin x}{2^n\sin \frac{x}{2^n}}=\cos \frac{x}{2}\cos \frac{x}{4}\cos \frac{x}{8}\cos \frac{x}{16}\cdots \cos \frac{x}{2^n}$$

Viete realized that as $n$ gets really large, the function $2^n\sin (x/2^n)$ starts to look a lot like the function $x$…and making this replacement in the formula as we let $n$ go to infinity yields

Proposition 2.5 (Viète’s Trigonometric Identity) $$\frac{\sin x}{x}=\cos \frac{x}{2}\cos \frac{x}{4}\cos \frac{x}{8}\cos \frac{x}{16}\cdots$$

An incredible, infinite trigonometric identity! Of course, there’s a huge question about its derivation: are we absolutely sure we are justified in making the denominator there equal to $x$? But carrying on without fear, we may attempt to plug in $x=\pi /2$ to both sides, yielding

$$\frac{2}{\pi }=\cos \frac{\pi }{4}\cos \frac{\pi }{8}\cos \frac{\pi }{16}\cos \frac{\pi }{32}\cdots$$

Now, we are left just to simplify the right hand side into something computable, using more trigonometric identities! We know $\cos \pi /4$ is $\frac{\sqrt{2}}{2}$, and we can evaluate the other terms iteratively using the half angle identity:

$$\cos \frac{\pi }{8}=\sqrt{\frac{1+\cos \frac{\pi }{4}}{2}}=\sqrt{\frac{1+\frac{\sqrt{2}}{2}}{2}}=\frac{\sqrt{2+\sqrt{2}}}{2}$$

$$\cos \frac{\pi }{16}=\sqrt{\frac{1+\cos \frac{\pi }{8}}{2}}=\sqrt{\frac{1+\frac{\sqrt{2+\sqrt{2}}}{2}}{2}}=\frac{\sqrt{2+\sqrt{2+\sqrt{2}}}}{2}$$

Substituting these all in gives the original product. And, while this derivation has a rather dubious step in it, the end result seems to be correct! Computing the first ten terms of this product on a computer yields $0.63662077105\dots$, wheras $2/\pi =0.636619772$. In fact, Viete used his own formula to compute an approximation of $\pi$ to nine correct decimal digits. This leaves the obvious question, Why does this argument work?

2.3 The Infinitesimal Calculus

In trying to formalize many of the above arguments, mathematicians needed to put the calculus steps on a firm footing. And this comes with a whole collection of its own issues. Arguments trying to explain in clear terms what a derivative or integral was really supposed to be often led to nonsensical steps, that cast doubt on the entire procedure. Indeed, the history of calculus is itself so full of confusion that it alone is often taken as the motivation to develop a rigorous study of analysis. Because we have already seen so many other troubles that come from the infinite, we will content ourselves with just one example here: what is a derivative?

The derivative is meant to measure the slope of the tangent line to a function. In words, this is not hard to describe. But like the sine function, this does not provide a means of computing, and we are looking for a formula. Approximate formulas are not hard to create: if $f(x)$ is our function, and $h$ is some small number the quantity

$$\frac{f(x+h)-f(x)}{h}$$

represents the slope of the secant line to $f$ between $x$ and $h$. For any finite size in $h$ this is only an approximation, and so thinking of this like Archimedes did his polygons and the circle, we may decide to write down a sequence of ever better approximations:

$$D_n=\frac{f(x+\frac{1}{n})-f(x)}{\frac{1}{n}}$$

and then define the derivative as the infiniteth term in this sequence. But this is just incoherent, taken at face value. If $1/n\to 0$ as $n\to \mathrm{\infty }$ this would lead us to

$$\frac{f(x+0)-f(x)}{0}=\frac{0}{0}$$

So, something else must be going on. One way out of this would be if our sequence of approximates did not actually converge to zero - maybe there were infinitely small nonzero numbers out there waiting to be discovered. Such hypothetical numbers were called infinitesimals.

Definition 2.3 (Infinitesimal) A positive number $ϵ$ is infinitesimal if it is smaller than $1/n$ for all $n\in \mathbb{N}$.

This would resolve the problem as follows: if $dx$ is some infinitesimal number, we could define the derivative as

$$D=\frac{f(x+dx)-f(x)}{dx}$$

But this leads to its own set of difficulties: its easy to see that if $ϵ$ is an infinitesimal, then so is $2ϵ$, or $kϵ$ for any rational number $k$.

Exercise 2.4 Prove this: if $ϵ$ is infinitesimal and $k\in \mathbb{Q}$ show $kϵ$ is infinitesimal$.

So we can’t just say define the derivative by saying “choose some infinitesimal $dx$” - there are many such infinitesimals and we should be worried about which one we pick! What actually happens if we try this calculation in practice, showcases this.

Let’s attempt to differentiate $x^2$, using some infinitesimal $dx$. We get

$$(x^2{)}^{\prime }=\frac{(x+dx{)}^2-x^2}{dx}=\frac{x^2+2xdx+d{x}^2-x^2}{dx}$$ $$=\frac{2xdx+d{x}^2}{dx}=2x+dx$$

Here we see the derivative is not what we expected, but rather is $2x$ plus an infinitesimal! How do we get rid of this? One approach (used very often in the foundational works of calculus) is simply to discard any infinitesimal that remains at the end of a computation. So here, because $2x$ is finite in size and $dx$ is infinitesimal, we would just discard the $dx$ and get $(x^2{)}^{\prime }=2x$ as desired.

But this is not very sensible: when exactly are we allowed to do this? If we can discard an infinitesimal whenever its added to a finite number, shouldn’t we already have done so with the $(x+dx)$ that showed up in the numerator? This would have led to

$$\frac{(x+dx{)}^2-x^2}{dx}=\frac{x^2-x^2}{dx}=\frac{0}{dx}=0$$

So, the when we throw away the infinitesimal matters deeply to the answer we get! This does not seem right. How can we fix this? One approach that was suggested was to say that we cannot throw away infinitesimals, but that the square of an infinitesimal is so small that it is precisely zero: that way, we keep every infinitesimal but discard any higher powers. A number satisfying this property was called nilpotent as nil was another word for zero, and potency was an old term for powers ($x^2$ would be the *second potency of $x$).

Definition 2.4 A number $ϵ$ is nilpotent if $ϵ\ne 0$ but ${ϵ}^2=0$.

If our infinitesimals were nilpotent, that would solve the problem we ran into above. Now, the calculation for the derivative of $x^2$ would proceed as

$$\frac{(x+dx{)}^2-x^2}{dx}=\frac{x^2+2xdx+d{x}^2-x^2}{=}\frac{2xdx+0}{dx}=2x$$

But, in trying to justify just this one calculation we’ve had to invent two new types of numbers that had never occurred previously in math: we need positive numbers smaller than any rational, and we also need them (or at least some of those numbers) to square to precisely zero. Do such numbers exist?